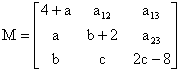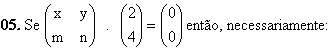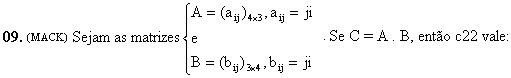Karla Diniz

Multiplicação de matrizes


A multiplicação de matrizes é realizada de acordo com a seguinte condição: o número de colunas da 1ª matriz deve ser igual ao número de linhas da 2ª matriz. Observe alguns modelos de matrizes que podem ser multiplicadas, considerando o formato m x n. 

A_4x3 . B_3x1 

A_4x2 . B_2x3 

A_1x2 . B_2x2 

A_3x4 . B_4x3 


Nesse modelo de multiplicação, os métodos são mais complexos. Dessa forma, precisamos ter muita atenção na resolução de uma multiplicação de matrizes. Vamos através de exemplos, demonstrar como efetuar tais cálculos. A operação deverá ser feita multiplicando os membros da linha da 1º matriz pelos membros da coluna da 2º matriz, onde os elementos devem ser somados, constituindo um único item posicional da matriz.Observe um modelo padrão de multiplicação:

Exemplo:

Realizamos uma multiplicação entre uma matriz A de ordem 2 x 3 por uma matriz B de ordem 3x2. Observe que a condição “o número de colunas da 1ª matriz deve ser igual ao número de linhas da 2ª matriz”, foi válida, pois 3 = 3. O interessante é que a matriz, produto da multiplicação, é de ordem 2 x 2, isto é, 2 linhas e 2 colunas, possuindo o mesmo número de linhas da 1ª e o mesmo número de colunas da 2ª. 

Portanto, todas essas condições são observadas na multiplicação entre matrizes. Caso alguma dessas condições não seja válida, a operação da multiplicação estará efetuada de forma incorreta. Sempre que realizar multiplicação entre matrizes, faça de forma atenciosa, desenvolvendo completamente o processo, procurando não utilizar meios diretos para obter o resultado. 

Aqui, uma vídeo-aula explicando melhor a multiplicação de matrizes.

Juliana

Exercícios de matrizes

 Questões:

01. Obter a matriz A = (aij)2x2 definida por aij = 3 i - j.


02. Se A é uma matriz quadrada de ordem 2 e A^t sua transposta, determine A, tal que A = 2 . A^t.


03. (UNIV. CATÓLICA DE GOIÁS) Uma matriz quadrada A é dita simétrica se A = A^T e é dita anti-simétrica se A^T = -A, onde A^T é a matriz transposta de A. Sendo A uma matriz quadrada, classifique em verdadeira ou falsa as duas afirmações:

(01) A + A^T é uma matriz simétrica
(02) A - A^T é uma matriz anti-simétrica


04. Se uma matriz quadrada A é tal que A^t = -A, ela é chamada matriz anti-simétrica. Sabe-se que M é anti-simétrica e:

Os termos a12, a13 e a23 de M, valem respectivamente:

a) -4, -2 e 4
b) 4, 2 e -4
c) 4, -2 e -4
d) 2, -4 e 2
e) 2, 2 e 4
 

a) x = y = 0
b) x = y = m = n = 0
c) x = y e m = n
d) y = -2x e n = -2m
e) x = -2y e m = -2n


06. Na confecção de três modelos de camisas (A, B e C)  são usados botões grandes (G) e pequenos (p). O número de botões por modelos é dado pela tabela:

	Camisa A	Camisa B	Camisa C
Botões p	3	1	3
Botões G	6	5	5

O número de camisas fabricadas, de cada modelo, nos meses de maio e junho, é dado pela tabela:

	Maio	Junho
Camisa A	100	50
Camisa B	50	100
Camisa C	50	50

Nestas condições, obter a tabela que dá o total de botões usados em maio e junho.

RESOLUÇÃO:

07. Sobre as sentenças:

I.   O produto das matrizes A3 x 2 . B2 x 1 é uma matriz 3 x 1.
II.  O produto das matrizes A5 x 4 . B5 x 2 é uma matriz 4 x 2.
III. O produto das matrizes A2 x 3 . B3 x 2 é uma matriz quadrada 2 x 2

É verdade que:

a) somente I é falsa;
b) somente II é falsa;
c) somente III é falsa;
d) somente I e III são falsas;
e) I, II e III são falsas.


08. (MACK) Se A é uma matriz 3 x 4 e B uma matriz n x m, então:

a) existe A + B se, e somente se, n = 4 e m = 3;
b) existe AB se, e somente se, n = 4 e m = 3;
c) existem AB e BA se, e somente se, n = 4 e m = 3;
d) existem, iguais, A + B e B + A se, e somente se, A = B;
e) existem, iguais, AB e BA se, e somente se, A = B.

 
a) 3
b) 14
c) 39
d) 84
e) 258


10. (PUC) Se A, B e C são matrizes quadradas e At, Bt e Ct são suas matrizes transpostas, e igualdade falsa entre essas matrizes é:

a) (A = B) . C = A . C + B . Cb) (A + B)^t = A^t + B^t

c) (A . B)^t = A^t . B^t

d) (A - B)C = AC - BC

e) (A^t)^t = A

Resolução:

01.

02.

03. (01) verdadeira
      (02) verdadeira

04. B

05. E

06.

	Maio	Junho
Botões p	500	400
Botões G	1100	1050

07. B

08. C

09. D

10. C

fonte: http://www.coladaweb.com/exercicios-resolvidos/exercicios-resolvidos-de-matematica/matrizes

Veronica

Representamos por aⁿ, a potência de base real a e expoente inteiron.

Definimos a potência an nos casos abaixo:

• 1º caso: Expoente inteiro maior que 1.

Potência de expoente inteiro maior que 1 é o produto de tantos fatores iguais à base quantas forem as unidades do expoente.

Assim:

  

Exemplos:

a) 4³ = 4 · 4 · 4 = 64

b) 1⁵ = 1 · 1 · 1 · 1 · 1 = 1

c) (–2)⁴= (–2) · (–2) · (–2) · (–2) = 16

D)

    

• 2º caso: Expoente 1

Toda potência de expoente 1 é igual à base.

Assim:

Exemplos

a) 5¹ = 5

b)

      

• 3º caso: Expoente zero

Toda potência de expoente zero é igual a 1.

Assim:

Exemplos

a) 5⁰ = 1

b)= 1

• 4º caso: Expoente inteiro negativo

Toda potência de expoente inteiro negativo e base não-nula é igual à potência de base igual ao inverso da base dada e expoente igual ao oposto do expoente dado.

Assim:

Exemplos:

a) 

 

b) 

   

c) 

    

Observação:

Sendo n um número inteiro, temos:

1a)  a = 0 e n > 0 -> aⁿ = 0
2a)  a = 0 e n < 0 ->  aⁿ  R
3a)  a > 0 -> aⁿ > 0
4a)  a < 0 e n par -> aⁿ > 0
5a)  a < 0 e n ímpar -> aⁿ < 0

2. Propriedades

Consideremos os números reais a e b, e os números naturais m e n. Então são válidas as seguintes propriedades.

• P1: Produto de potências de mesma base

Para multiplicarmos potências de mesma base, conservamos a base e somamos os expoentes.

Justificativa:

 =

Assim: a^m · aⁿ = a^m+n.

Exemplos:

a) 2³ · 2⁵ = 2³⁺⁵ = 28

b) 4^x · 4^-x+2 = 4^x+(-x+2) = 42

c) 3 · 3² · 3⁶ = 3¹⁺²⁺⁶ = 39

• P2: Quociente de potências de mesma base

Para dividirmos potências de mesma base, conservamos a base e subtraímos os expoentes.

Justificativa:

1o. Sendo m > n, temos

2o. Se m = n,  = 1= a^(m-n) = a⁰ = 1

3o. Se

                  

 = a (m - n)

Exemplos:

a) = 2^6-2 = 24

b) 

 = 5^x-2

c) 

 = 4^(x+2)-(x-3) = 45

• P3: Produto de potências de mesmo expoente

Para multiplicarmos potências de mesmo expoente, conservamos o expoente e multiplicamos as bases.

   

   

Justificativa

   

               

          

Assim: aⁿ · bⁿ = (ab)ⁿ.

Exemplos

a) 2⁴ · 8⁴ = (2 · 8)⁴ = 16⁴

b) x³ · y³ · z³ = (x · y · z)³

• P4: Quociente de potências de mesmo expoente

Para dividirmos potências de mesmo expoente, conservamos o expoente e dividimos as bases.

Justificativa:

Assim:

   

Exemplos:

a)   

    

b)    

• P5: Potência de uma potência

Para elevarmos uma potência a um novo expoente, conservamos a base e multiplicamos os expoentes.

  

Justificativa:

  

  

Exemplos:

a) (23)² = 2^2.2 = 26

b)= 3^2.3.2 = 3¹²

Observação

As propriedades apresentadas podem ser estendidas para os expoentes m e n inteiros.

Exemplos

a) 2³ · 2^-2 = 2^{3 + (-2)} = 2¹ (P1)

b) = 5^{2 - (-3)} = 5^{2 + 3} = 5⁵ (P2)

c) 5^-3 · 2^-3 = (5 · 2)^-3 = 10^-3 (P3)

d) (P4)

e)  (P5)

Situações Especieais

A. (– a)ⁿ  e  –aⁿ

As potências (–a)ⁿ e –aⁿ , em geral, apresentam resultados diferentes, pois:

 Exemplos

a) (–2)⁴ = (–2) · (–2) · (–2) · (–2) = 16

b) –2⁴ = – 2 · 2 · 2 · 2 = –16

c) (–2)³ = (–2) · (–2) · (–2) = –8

d) –2³ = – 2 · 2 · 2 = –8

B.

  

As potências , em geral, apresentam resultados diferentes, pois:

  

e

Exemplos

a)= (32) · (32) · (32) = 32 · 3 = 36

b)= 32 · 2 · 2 = 38